Операторы генетических алгоритмов
А' = a1, a2, … , ak,a'k+1,…, a'L (4)' = a'1, a'2, … , a'k,ak+1,…, aL (5)
После применения OK имеем две старые хромосомы и всегда получаем две новые хромосомы. Схематически простой ОК показывает преобразование двух хромосом и частичный обмен информацией между ними, используя точку разрыва, выбранную случайно.
В двухточечном ОК определяются две точки ОК, и гены обмениваются между ними. Например:

Рисунок 2 - Двухточечный ОК
Отметим, что точки ОК в двухточечном ОК также определяются случайно. Существует много модификаций двухточечного ОК.
Развитием двухточечного ОК является многоточечный ОК или N-точечный ОК, он выполняется аналогично двухточечному ОК, хотя большое число «разрезающих» точек может привести к потере «хороших» родительских свойств.
Порядковый ОК. В порядковом ОК «разрезающая» точка также выбирается случайно. Далее происходит копирование левого сегмента р1 в р'1. Остальные позиции в р'1 берутся из р2 в упорядоченном виде слева направо, исключая элементы, уже попавшие в р'1. Например:
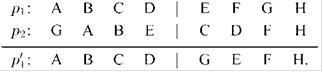
Рисунок 3 - Порядковый ОК
Получение р'2 может выполняться различными способами. Наиболее распространенный метод - копирование левого сегмента из р2, а далее анализ р1 методом, указанным выше. Тогда имеем р'2 : (G А В Е | С D F Н).
Частично-соответствующий ОК. Здесь также случайно выбирается «разрезающая» точка или точка ОК. Дальше анализируются сегменты в обоих родителях, и устанавливается частичное соответствие между элементами первого и второго родителей с формированием потомков. При этом правый сегмент р2 переносится в р'1, левый сегмент р1 переносится в р'1 с заменой повторяющихся генов на отсутствующие (гены, находящиеся в частичном соответствие). Например:
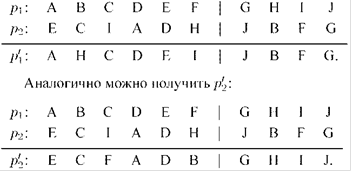
Рисунок 4 - Частично-соответствующийОК
Циклический ОК. Циклический OK выполняет рекомбинации согласно циклам, которые существуют при установлении соответствия между генами первого и второго родителей. Например, пусть популяция Р состоит из двух хромосом Р = {р1,р2}. Первый и второй родители и их потомок имеют вид:

Рисунок 5 - Циклический ОК
Универсальный ОК. В настоящее время он популярен для решения различных задач теории расписаний. Вместо использования разрезающей точки (точек) здесь определяют двоичную маску, длина которой равна длине заданных хромосом. Получение потомков выполняется на основе правил сложения булевой алгебры соответствующих генов родителей и маски (0 + 0 = 0, 0 + 1 = 1, 1 + 1=0). Для каждого элемента в p1, р2 гены меняются, как показано на следующем примере:
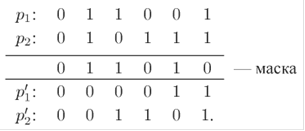
Рисунок 6 - Универсальный ОК
Маска обычно выбирается случайно с заданной вероятностью или на основе генератора случайных чисел. При этом чередование 0 и 1 в маске происходит с вероятностью «0,5 (т. е. приблизительно в 50% случаев). В некоторых случаях используются параметризированный универсальный ОК, где маска может выбираться с вероятностью для 1 или 0 выше, чем 0,5. Такой вид маски эффективен, когда хромосомы кодируются в двоичном алфавите.
В оптимизационных задачах находят применение различного типа «жадные» операторы кроссинговера. Они основаны на анализе ЦФ решений после каждого шага «жадного» ОК. Он может быть реализован на двух и более хромосомах, а в пределе - на всей популяции. Приведем типичный модифицированный алгоритм «жадного» ОК:
. Для всех хромосом популяции вычисляется ЦФ. Выбирается заданное число родительских хромосом, и случайным образом на одной из хромосом определяется точка «жадного» ОК.
. В выбранной хромосоме для i-го гена, расположенного слева от точки «жадного» ОК, определяется частичная ЦФ, т. е. стоимость пути от i-гo гена к рядом находящемуся гену. Аналогичные действия выполняются по определению стоимости пути во всех остальных хромосомах, выбранных для «жадного» ОК.
. В хромосому «потомок» выбирают тот ген, у которого значение ЦФ выше (ниже) при максимизации (минимизации) ЦФ.
. Процесс продолжается, пока не будет построена хромосома «потомок». Если в процессе реализации «жадного» О К возникает цикл или тупик, то в потомок выбираются нерассмотренные гены с лучшей ЦФ.
