Линейная производственная функция комплексного аргумента

Обычно в теории производственных функций переменными выступают объём производства Q, затраты труда L и затраты капитала K, как наиболее существенные факторы, и результат производства. Из множества производственных ресурсов выбираются эти два - труд и капитал, поскольку до определённой степени они являются взаимозаменяемыми - один и тот же объём производства Q может быть достигнут при разных соотношениях K и L и неизменном количестве прочих производственных ресурсов. Представим производственные ресурсы K и L в виде комплексной переменной .

Тогда производственная функция в общем виде будет выглядеть так:

.

Здесь K, L, и Q - положительные действительные числа. Отнесение K в действительную часть, а L - в мнимую условно и не играет принципиального значения. В такой функции комплексному числу сопоставляется действительное число Q.

В простейшем случае связать затраты труда L и капитала K с результатами производства Q можно следующим образом [8, 10]:

.(2.1)

Здесь a0 и a1 - действительные числа. Первый сомножитель, представляющий собой комплексное число , помогает связать в одной модели производственные затраты и результаты, но требует самостоятельного научного исследования.

Осуществляя перемножение сомножителей в правой части равенства (2.1) и группируя вещественную и мнимую части, получим:

.(2.2)

В результате имеем комплексное число, вещественная часть которого равна Qt, а мнимая часть должна быть равна нулю в силу того, что в левой части равенства мнимой части нет, то есть она представлена произведением i0. Следовательно, производственная функция (2.1) представляет собой аддитивную модель вида:

,(2.3)

где коэффициенты а0 и а1 представляют собой части одного комплексного числа.

Именно последнее обстоятельство предопределяет особенность свойств предложенной модели производственной функции комплексного аргумента. Использовать просто модель (2.3) в данном случае нельзя, поскольку должно выполняться ещё и условие

.(2.4)

Решение системы уравнений (2.3) и (2.4) позволяет найти искомые значения коэффициентов а0 и а1. Но тот же самый результат можно получить и используя непосредственно модель (2.1). Для этого определим комплексное число коэффициентов через объёмы и ресурсы, сделав несколько элементарных преобразований:

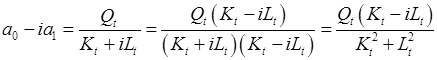,(2.5)

Полученное равенство, как это следует из свойств комплексных чисел, выполняется только в том случае, когда равны друг другу вещественные и мнимые части комплексных чисел в его левой и правой частях. Это свойство позволяет легко получить формулы для расчёта коэффициентов. Действительно, раскрывая скобки и группируя отдельно вещественную и мнимую части, получаем формулы для вычисления каждого из коэффициентов: