Анализ коэффициентов линейной производственной функции комплексного аргумента предприятия ООО «Ресурс»

.(2.10)

С учётом неотрицательности переменных, получаем, что и коэффициенты а0, и а1 принимают свои максимальные значения только в том случае, когда относительное значение затрат труда равно относительному значению затрат капитала, то есть:

.(2.11)

Учитывая (2.11), из формулы для вычисления коэффициентов (2.6), легко найти максимальные значения коэффициентов:

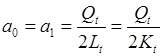.(2.12)

Итак, можно сделать вывод о том, как меняются значения коэффициентов использования ресурсов.

Коэффициент а1 при фиксированном положительном значении ресурса Кt равен нулю при равенстве нулю ресурса Lt; коэффициент а0 при этом больше нуля. При возрастании трудовых затрат Lt от нуля до значения, определяемого равенством (2.11) коэффициент а1 возрастает. При значениях ресурса Lt, равного ресурсу Кt, коэффициент а0 достигает своего максимального значения (2.12). При этом его значения равны коэффициенту а1. С дальнейшим ростом значений трудовых ресурсов коэффициент а0 уменьшается и стремится к нулю при стремлении значений Lt к бесконечности. На этом участке коэффициент а0, в силу (2.7), всегда больше коэффициента а1, который также уменьшается с ростом Lt .

Таким же образом в зависимости от капитальных ресурсов Кt ведёт себя и другой коэффициент - коэффициент использования капитальных ресурсов.

На рисунке 2.1 изображен график изменения коэффициента а1 в зависимости от изменения значений трудовых ресурсов при фиксированном положительном Кt.

Любая производственная единица, будь то отдельно взятое предприятие или хозяйство всей страны, развивается во времени. При этом меняются технологии производства, вызывая изменения производительности труда и производительности оборудования. Эти изменения отражаются в производственной функции изменением коэффициентов использования ресурсов. [12]

С этих позиций коэффициенты a0 и а1 можно рассмотреть как некоторые функции от времени: а1=f1(t), а0=f0(t). Но так как указанные коэффициенты являются частями одного комплексного числа, то эти зависимости следует рассмотреть в комплексе. То есть, рассматривая коэффициенты в динамике, следует найти зависимость

.(2.13)

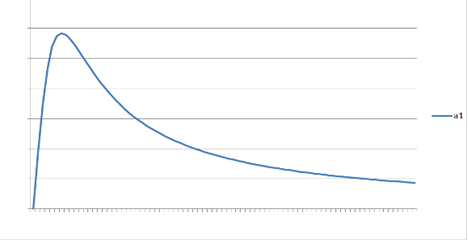
Рисунок 2.1. График зависимости а1 от Lt

Рассмотрим эту задачу с помощью графического метода, поскольку данное комплексное число может быть отображено на плоскости (а0, а1), где коэффициенты использования ресурсов выступают в качестве осей координат данной плоскости.

Динамика изменения комплексного числа во времени может иметь самый различный вид, но если эта динамика может быть описана в виде зависимости

,(2.14)

то она представляет особый интерес.

С учётом того, что в теории производственных функций за точку отсчёта принимаются начальные значения динамических рядов, их относительные значения будут равны единице, а это означает, что в начальной точке коэффициенты а0 и а1 будут равны друг другу и равны 0,5 (как это следует из (2.6)).

В теории производственных функций принята именно эта точка отсчёта, поэтому в дальнейшем будем считать, что все исходные переменные приведены к начальным значениям. Иные случаи будут оговорены отдельно.