Отбор главных факторов

Процедура отбора главных факторов включает следующие этапы.

Анализ факторов на мультиколлинеарность и ее исключение. Определение мультиколлинеарности проводится путем анализа значений коэффициентов парной корреляции rij между факторами xi xj. Если ½rij½>0,7, то факторы xi xj - мультиколлинеарны.

Для получения коэффициентов парной корреляции вычислим корреляционную матрицу. Для этого выберем команду «Анализ данных» и функцию «Корреляция». В раскрывшемся окне «Корреляция» в строке «Входной интервал» введем интервал ячеек со значениями переменных. [18]

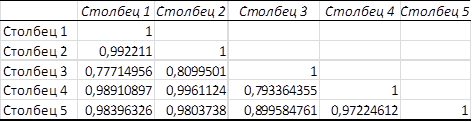
Рисунок. 3.2. Корреляционная матрица

Из рисунка 3. 2 видно, что мультиколлинеарность присутствует между всеми факторами.

Для устранения мультиколлинеарности один из факторов исключим из модели. Факторы, подлежащие исключению, определяются в ходе оценки следующих статистических характеристик: коэффициента парной корреляции между фактором и функцией (rx,y); коэффициента bk - фактора k, критерия Стьюдента (tk).

. Анализ факторов на мультиколлинеарность и ее исключение.

Здесь проводится анализ значений коэффициентов парной корреляции rij между факторами хi и хj.

. Анализ тесноты взаимосвязи факторов (х) с зависимой переменной (у).

Для проведения этого анализа используюем значения парной корреляции между фактором и функцией (rx,y). Величина rx,y также представлена в корреляционной матрице. Факторы, для которых rx,y=0, т.е. не связанные с у, подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение ½rij½, могут быть потенциально исключены из модели. В нашем случае все факторы мультиколлинеарены между собой. Однако х1 имеет наибольшую тесноту связи с у, rx,y =0,984 и его можно оставить для дальнейшего анализа. Остальные факторы потенциально могут быть исключены из анализа. Вопрос об их окончательном исключении решается в ходе анализа других статистических характеристик. Для измерения мультиколлинеарности можно использовать коэффициент множественной детерминации: Д=R2, где R - коэффициент множественной корреляции.

. Анализ коэффициентов b факторов.

Для того чтобы определить, какие факторы подлежат исключению проведем анализ коэффициентов b факторов.

Коэффициент b указывает влияние анализируемых факторов на у с учетом различий в уровне их колеблемости

где bk - коэффициент b k - го фактора;

sxk - среднеквадратическое отклонение k -го фактора;

sy - среднеквадратическое отклонение функции;

ak - коэффициент регрессии при k - м факторе.

Для расчета коэффициентов b предварительно необходимо рассчитать среднеквадратическое отклонение (в Excel оно называется стандартным отклонением) факторов и функции.

Воспользуемся функцией «СТАНДАРТОТКЛОН» для расчёта среднеквадратического отклонения.

Таблица 3.2