Отбор главных факторов

По формуле 3.2 найдем значения bk.

Таблица 3.3

Из двух факторов хi и хj может быть исключен тот фактор, который имеет меньшее значение b, поэтому можем отбросить факторы x2, x3 и x4.

Проверим коэффициенты регрессии на статистическую значимость. Проверка статистической значимости ak производится двумя способами: по критерию Стьюдента и по критерию Фишера. Для проверки статистической значимости ak по критерию Стьюдента tk рассчитывают по следующей формуле

где ak - коэффициент регрессии при k - ом факторе, Sak - стандартное отклонение оценки параметра ak. [20]

Критерий Стьюдента уже был вычислен при выполнении функции регрессии (см. Лист «Регрессия 1», столбец «t - статистика», рис. 3.1).

Число степеней свободы статистики tk равно f=n-m-1, где m - количество факторов включенных в модель (f=12-4-1=7). Расчетное значение tk сравним с критическим значением tf,a, найденным по таблице 1 приложения 1. При заданном уровне значимости a (a=0,05) и числе степеней свободы f=7, в нашем примере t7,0.05=5,408.

Если tk³tf,a, то ak существенно больше 0, а фактор хk оказывает существенное влияние на у. При этом фактор хk оставляем в модели. Если tk<tf,a, то фактор исключаем из модели.

Проверка статистической значимости аk по критерию Фишера -

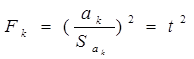,(3.4)

где t2 - многомерный аналог критерия Стьюдента. [15]

Число степеней свободы статистики Fk следующее: f1 = 4, f2=n-m-1. Значение Fk, вычисляемое по формуле, сравним с критическим значением Ff1f2a=4,13, найденным по таблице 2 приложения 3, при заданном уровне значимости a и числе степеней свободы f1 и f2.

Если Fk³Ff1f2a, то ak - существенно больше 0, а фактор xk оказывает существенное влияние на у. При этом фактор хk оставляем в модели. Если Fk<Ff1f2a, то фактор исключаем из модели. В результате следует исключить x2, x3 и x4.

Проанализируем факторы на управляемость. В ходе логического анализа на основе экономических знаний следует сделать вывод: можно ли разработать организационно - технические мероприятия, направленные на улучшение (изменение) выбранных факторов на уровне предприятия. Если это возможно, то данные факторы управляемы. Неуправляемые факторы на уровне предприятия могут быть исключены из модели.

Аналогично, описанному выше построим модель в которой будут следующие факторы: x2 и у. Для этой модели определим коэффициент множественной детерминации Д, который служит для измерения тесноты связи между x2 и у.

Д=R2=0,949.

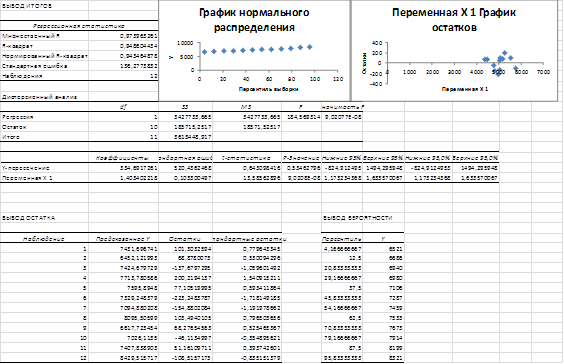
Рисунок 3.3. Лист «Регрессия 2»

Исходя из перечисленных выше суждений исключим фактор x4 так как он имеет наименьшее значение b. Построим корреляционную матрицу без исключенного фактора.