Отбор главных факторов

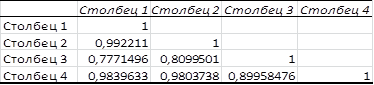
Рисунок 3.4. Корреляционная матрица без фактора x4

Из матрицы видно, что все факторы мультиколлинеарны. Далее исключим из модели фактор x3, так как он имеет наименьшую тесноту связи с y. По аналогии вычислим корреляционную матрицу без факторов x3 и x4.

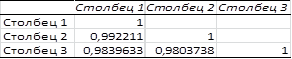
Рисунок 3.5. Корреляционная матрица без факторов x3 и x4

Опять же факторы мультиколлинеарны, поэтому в модели оставим один фактор x1.

Исследуем целесообразность исключения факторов из модели с помощью коэффициента детерминации.

Прежде чем вынести окончательное решение об исключении переменных из анализа в силу их незначимого влияния на зависимую переменную, произведем исследование совместного влияния факторов.

Для этого используется статистика, которая имеет F - распределение с f:

F=(3.5)

где Дm - коэффициент детерминации регрессии с m объясняющими переменными; Дm1 - коэффициент детерминации регрессии с m1 факторами; m - число переменных в первой регрессии; m1 - число переменных в последней регрессии.

Если Fрас.£Ff1f2a, то исключенные выше факторы совместно не оказывают статистически значимого влияния на функцию. Вычислим Fрас.:

Fрас.=

Определим критическое значение статистики F при f1=4-3=1 и f2=12-4-1=7 и уровне значимости a=0,05: F1,7,0.05=3.34, с помощью таблицы 2 приложения 1.

Получаем что 0<5,59, следовательно, ранее исключенные x2, x3, x4 факторы совместно не оказывают статистически значимого влияния на переменную у.