Быстрое преобразование Фурье длины 5

(24)

Рассмотрим преобразование Фурье длины в поле . Элементами этого преобразование должны быть элементы подгруппы, образованной примитивным элементом (в соответствии с таблицей 1). Перекодируем укороченный вектор (вектор длины 51) в полный вектор (длины 255) таким образом, чтобы все координаты , для которых , были нулевыми. Практически это означает, что мы разместим укороченный вектор только в одной плоскости БПФ-куба там, где . Тогда формулу (24) можно переписать в виде:

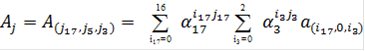
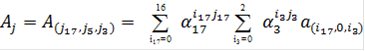(25)

А это означает переход к ДПФ с ядром для вектора . Преобразование Фурье вычисляется как значение многочлена в точках поля: , что эквивалентно работе в подгруппе с ядром : .

Очевидно, что для реализации БПФ-укорочения длины 85 с порождающим элементом из формулы (24) необходимо исключить суммирование по , что достигается путем размещения укороченного вектора в плоскости БПФ-куба там, где . Это означает переход к ДПФ с ядром для мультипликативной подгруппы порядка 85 с шагом 3.

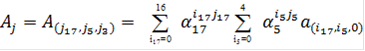
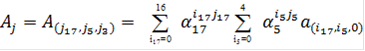(26)

Проводя аналогичные рассуждения можно построить формулы вычисления ДПФ для всех циклических подгрупп, указанных в таблице 1. Эти БПФ-укорочения можно применить для кодирования укороченными кодами Рида-Соломона над полем длин n=85,51,17,15,5,3.

Заключение

На основании китайской теоремы об остатках получен результат, существенно понижающий вычислительную сложность ДПФ. Приведены формулы для трехмерного преобразования Фурье поле . Построены алгоритмы быстрого преобразование Фурье (БПФ) длин 3, 5 и 17 на основе алгоритма Рейдера и алгоритма Винограда вычисления циклической свертки. Показана эквивалентность между вычислением ДПФ простой длины и вычислением циклической свертки.

На основании трехмерного преобразования Фурье построены укороченные преобразования длин 15, 51, 85, которые рационально применять, когда не требуется кодировать слова длины 255. Показана эквивалентность между укорочением преобразования и переходом на соответствующую ему подгруппу мультипликативной группы поля.

В приложении представлен программный комплекс, реализующий построение поля основные операции в этом поле, вычисление значения произвольного многочлена в любой точке поле, вычисление ДПФ, ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,85,51,15,17,5,3, кодирование кодом Рида-Соломона в частотной области.